Ayanamsa
The points of intersection of the Sun’s apparent path with the Celestial Equator, which of the Precession is stated to be not coincident but recede, are called the Precession of the Equinoxes. When the moving Zodiac coincided with the fixed Zodiac is anybody’s guess. In the past, many learned astronomers and astrologers bestowed their serious attention on this aspect and arrived at varying results. Even now, almost everyone has his own pet value. It is time that uniformity is reached so that it could be taken as a standard.
Get Various Ayanamsas Calculations with LifeSign Astrology Software
In dealing with the problem of the Precession of the Equinoxes there are two things to be settled. Firstly, the rate of Precession and secondly, the date of Precession. There were differences of opinion even among the ancient Western scholars in the matter. The Platonic Year or the Great Period was stated differently as follows:
Tycho —————————–25,816 years
Ricciolus——————————-25,920 years
Cassini———————————-24,800 years
Normen Lockyer————————–24,450 years
According to the Hindu Siddhantas, the rate of the Precession is stated to be:
Aryabhatta —————————- 46″-3
Parasara —————————- 46″ *5
Varahamihira —————————— 50″ *0
Surya Siddhanta —————————— 54″ *0
Vriddha Vasishta ——————————- 54″-0
Manjula and Bhaskara ——————————- 59″ 9
Grahalaghavam ————————————— 60″ 0
This shows how varied the opinions were. No doubt, the Vernal Point undergoes a good deal of wobbling in the course of a year, but still an average rate of Precession could be worked out for a sufficiently long period. This was done by Prof. Simon Newcomb and his formula was based on values tabulated from 1600 A.D. to 2100 A.D. According to him, the earth completes one precession cycle in 25,794 years for the epoch of 1844. His formula is 50 “.2453 plus (0”.0002225) multiplied by the required year, 1850 A.D. This is scientific and has been accepted by the vast majority of people. My view is also that this rate of Precession could The next question is that of fixing the date of the coincidence of both the Zodiacs.
In the determination of the exact time of co-incidence of both the Zodiacs learned astronomers and astrologers have exhausted almost all possible angles. My purpose here is not to evolve a new theory adding to the confusion, but only to suggest a way to choose from among the several theories that one which is most appealing. A study of various opinions shows a surprisingly big margin of 886 years involving 12°.3 in the Ayanamsa value. But such a big margin could be reduced by analytical reasoning of the various periods suggested. The following tabulation shows the spread in the dates assigned by various authorities:
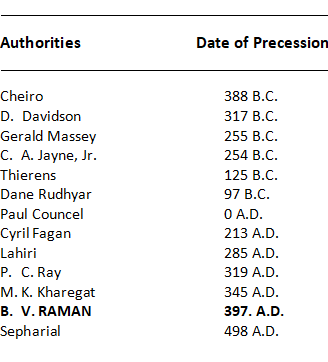
Without discussing the individual views of the first six who have taken the periods before the Christian Era, I surmise that the) fixed the dates basing their calculations on the Egyptian Zodiac. The first recorded Zodiacal Year of Egypt started in 4699 B.C. At that time the Egyptian Zodiac had six constellations of 60 degrees each. Later, a secondary system of twelve constellations of 30 degrees each came into use from 4000 B.C. At about 1 “SO B.C. a compromised system of 12 irregular constellations was adopted. In 4699 B.C., the Pyramid’s meridian was marked at the toe of 6 Castor and then again in 4000 B.C.. it cut the Bull’s horns.
Apparently, the above authorities have made their calculations from these points and dates, and they cannot yield correct results as there was confusion in the Egyptian Zodiac itself in those days. Again, the process is not scientific. Hence, it seems to me that the first six dates cannot be taken as conclusive.
Some scholars are inclined to base their theories on notable mundane events. Alan Leo says: When the Sun enters Pisces, the sign of the fishes, there came the Saviour Jesus, whose twelve disciples were fishermen. He himself being born of the virgin sign Virgo, opposite to Pisces.
“Paul Councel has apparently adopted 0 A.D. on this ground. It cannot be said whenever the Precession point touches a sign there will be the birth of a religion or a prophet or a savior. There is nothing on record to show that there was a similar birth when it touched Aries. Owing to the plurality of causes the date of any other notable mundane event cannot be taken as a pointer.” There are many who are inclined to calculate from the date of Varahamihira, as he makes a statement in Brihat Samhita that both the Zodiacs coincide in his time. However, the late Prof P S Sastri would say: “We are told by the great Varahamihira that he had found the entry of the Sun into 273° 20′ as beginning of the Uttarayana as against the Vedanga Jyotishcu Varahamihira died in 509 Saka or 41 B.C.”
This point is controversial.
Sephaml says: “By reference to various Sanskrit cmd vernacular works, we have decided, in common with many competent Pandits, that the two 7odjacs exactly coincide in the year of the Kaiiynga 3600. And this agrees with the obsess: ** Mihira in his Samhita, where commerr.K? on the phenomenon of the Precession of Equinoxes he states that in his day. the Summer Solstice coincided with the first degree of Kataka (Cancer). .. Kali Yuga began in February B.C. 3102. Therefore, to obtain the date of the coinciding of the Zodiacs, we say 3600 – 3102 = A.D. 498 which falls within the limits of the period ascribed to Mihira and thus, supports his independent statement and observation. ”
Mr. Chidambara Iyer also opines that Varahamihira’s time was between 416 and 572 A.D. Still others are of the opinion that he was born in 505 A.D. and died in 587 A.D. They come to this conclusion since Varahamihira quotes Aryabhatta who was born in 476 A.D. only. Thus, any evidence-based on Varahamihira’s time is highly controversial and not reliable. Further, he has not given any astronomical data for his calculations. Sepharial has also stated elsewhere that according to Bhaskaracharya in his Graha Ganitadhyaya the Vernal Equinox of Kali Yuga 3628 (A.D. 527) coincide. These only show that the Siddhantas were not uniform in their conclusions and that no astronomical basis was given by Sepharial or the dates of Siddhantas are acceptable. Dr. B.V.Raman has followed, as Mr. Sastri says, Surya Siddhanta. It is seen that the Indian year is longer than the European estimate by 3 minutes and 20-4 seconds. The average rate of the Precession of 5013 seconds adopted by him is also approximate. Hence, his figure does not appeal to me.
At the close of the 19th century, many were inclined to compute from the position of Zeta Piscium. The idea sprang up because of the statement of Surya Siddhanta that the sidereal revolution of a planet ends with the fixed star Revati which marks the end of the sign Pisces What is stated here is that the Zodiac ends with the end of Revati star, which has vanished now. and not its centre. Further, as Mr. Chidambara Iyer has stated, Zeta Piscium is not Revati and it is also not in the ecliptic and that any calculation made on this will not yield correct results.
The star Aswini marks the beginning of the Fixed Zodiac, but there is no identifiable star in the middle. Though Mr. P.C.Ray has worked out the year as 319 A.D., based on this star, ye: as remarked by Mr. M.K. Kharegat “the observational data are open to question and only an approximate estimate can be made.”
The calculations from the star Spica (Chitta) appear to be very appealing. Out of the stellar quarters of Chitta, two are in Virgo and the other two in Libra. The central point of the constellation Chitta is thus, the star Spica of the first magnitude. This is quite opposite the constellation Aswini’s central point, which marks the beginning of the Indian Zodiac. Hence, the calculations made from the star Spica will be perfect. Messrs. Lahiri and Kharegat advocate this method and my opinion also is that this method alone can stand the test of time. However, Mr. Kharegat differs from Mr. Lahiri by taking the polar longitude of Spica and not the celestial longitude. He says: “Ancient Indian and Arabic records give what is called the polar longitude and not the true or celestial longitudes as we do today.” While Mr. Kharegat is inclined to take the polar position of the star, he prefers to discard the other theories of the Siddhantas in the light of modern theories. All working methods should be uniform. The position of other planets, the rate of Precession, etc., have all been studied with reference to celestial longitudes only. Mr. Chidambara Iyer and many others are inclined not to follow the polar longitude. My view is also in agreement with them.
Prof. Sastri points out: “The various theories take for granted that the two Zodiacs coincided on a New Moon day which marks the beginning of the month Chaitra. Why should there be such an assumption?”
What is required is to find put the correct longitude of the star Spica and then to calculate its movements. In the past, the star Spica Virginis was observed as follows in longitude:
cases. ” Thus, Spica being a first magnitude star has an annual motion of 50″ plus 0″-25 totaling to 50″-25. To put it in a precise way, it agrees with Newcomb’s precessional value of 50-248
My opinion is that a correct calculation of the Ayanamsa can be made from the latest position of Spica itself, instead of beginning from the early centuries, when modern instruments were not available. The average Precession rate is 50″ without taking into account the motion of stars observed by Sepharial. He says: “Thus while Hipparchus and Ptolemy found it to be only 10 in 100 years. Albatani found it to be only 10 in 66 years and modern observations seem to point to the fact that it has been accelerated up to our own time. By taking a mean of all observations for the last 18 centuries the mean appears to be 50 062 and e can work it over by taking 50″ nearly.” Yarahamihira also supports this figure.
Robson observes thus, about Precession:
“The Precession of the Equinoxes is a phenomenon that causes all the stars to appear to advance in longitude in a body at the rate of 50” per annum due to the retrograde motion of the Vernal Equinox or First Point of Aries through the constellations. This precessional change does not affect the relative positions of the stars among themselves.” Besides the processional movement, each star has its own ‘proper motion’. About the proper motion, he observes: “As seen from the earth the average proper motion of a first magnitude star is about 0”.25 annum while that of a sixth magnitude star is about 0”-04 but the actual rates vary in individual cases, “Thus, Spica is a first magnitude star has an annual motion of 50” plus 0 “.25 totaling to 50 “.25. To put it in a precise way, it agrees with Newcomb’s precessional value of 50.2486.
In effect, the present position of Spica as per the Nautical Almanac minus 1800 will be the difference in the Ayanamsa that will have to be adopted. This method is simple, straight and reliable. Based on this principle, let me work out the present Ayanamsa with reference to the position of Spica given or 1820 A.D. by the Nautical Almanac:
The above will show that there is only a difference of 29 seconds between the above computation and Mr. Lahiri’s figure. This difference is probably, due to Mr. Lahiri’s having taken an adjusted Zero-year to fit in with a New Moon day and a Lunar New Year’s Day. It is also possible when Spica’s figure of 21° 20’ was taken for 1820 as per Nautical Almcmac a small fraction of a minute might have been either omitted or rounded off to a full minute. At any rate, the difference is negligible. C.G. Rajan has adopted the Ayanamsa of 23° 19’ in his Panchang for Subhakritu. Mr. V.Venkataramana Rao mentions the Bhujandar Nadi’s figure of 22° 44′ for 1926.
Working this out on Newcomb’s formula the Ayanamsa on 1-1-1962 is 23° 14’15”, which gives a difference of only 5 minutes.
In the previous paragraph, the figure given in the Nautical Almanac for 1820, only has been taken instead of Robson’s figure of 22° 43′ for 1920, since the latter too has omitted the fraction of a minute and the correct figure on 1-1-1920 was 22″ 43′ 43″. Taking the figure of Menclaus for 99 A.D., and working out the average rate of Precession of 50-2455225, the Ayanamsa on 1-1-1962 is 22° 15′ 7″. Adopting the same procedure for the Nautical Almanac’s year of 1820, it works out to 23° 18′ 54″ for J42 years. Thus, there is a difference of 1° 3′ 46″. However, applying Newcomb’s formula the Precession rate for 99 A.D. is 47″-8557. Working it out for 1863 years at the average rate of 47″-8559225, the Ayanamsa on 1-1-1962 is 21° 0’58”. There is thus, a difference of 2°17’55”. These differences in value when compared to 99 A.D. show that the positions noted in the olden days without the assistance of precession instruments might have been a little faulty. Further, this also shows that even after taking a fixed date, different sets of figures are inevitable if there is even a slight variation in the rate of Precession. Hence, an authentic figure based on the Nautical Almanac has been taken.
Summarising, 1 consider that the longitude of the star Spica as noted in the National Almanacs less 180 degrees could be taken as the value of Ayanamsa for each year, that its annual motion consists of not only the precessional motion but also its own proper motion and that Newcomb’s formula regarding the annual rate of the Precession could be adopted as standard. Accordingly, the Ayanamsa on 1st January 1962 is 23 18’ 54” which, it seems to me, could be standardized. In my personal experience, I have found that this figure uniformly gives correct results. (6-63).
Courtesy: Modern Astrology (S. Kannan)











